6 ноября 2004 года с 16.10 до 18.00
в аудитории 16-24 главного здания МГУ на Воробьёвых горах
Сергей Александрович ШАРОВ, архитектор-реставратор,
прочитает лекцию
НАДВРАТНЫЙ ХРАМ ИОАКИМА И АННЫ ВО ВЛАДИМИРЕ
(опыт историко-архитектурной реконструкции)
Основная цель лекции - демонстрация возможностей научной
историко-архитектурной реконструкции давно утраченных памятников.
Церковь Иоакима и Анны, построенная епископом Иоанном и князем
Всеволодом Большое Гнездо в 1195---1196 годах на воротах Детинца города
Владимира, давно утрачена. От неё практически не сохранилось даже
изображений (только рисунок воротной башни с надстроенной в XVII веке
на месте церкви колокольней), а археологические раскопки выявили лишь
основание башни ворот и позволили собрать небольшую коллекцию обломков
архитектурных деталей памятника, дающих самое общее представление о его
декоративном убранстве. Казалось бы, наши возможности реконструировать
облик храма равны нулю.
Однако, особенности техники строительства в полу-бутовой кладке,
практически не позволяющей возводить несущие стены толщиной менее
75 см, технические ограничения на отдельные элементы постройки
(минимальная ширина дверных проёмов и лестниц, предельный уклон
лестницы и т. п.) вкупе с тщательным анализом остатков памятника и его
близких архитектурных аналогов позволяют достоверно воссоздать
архитектурные формы и конструктивную структуру утраченной постройки,
скрупулёзно рассчитать её размеры и осуществить доказательную
реконструкцию с поразительной точностью (в пределах 5-10 см).
Полученная реконструкция, в свою очередь, объясняет происхождение ряда
загадочных особенностей знаменитых построек Ростовского кремля,
возведённых митрополитом Ионой Сысоевичем пятьсот лет спустя, в конце
XVII века.
Сергей Валерьевич МАРКЕЛОВ, учитель школы 57,
16 октября
прочитает лекцию на тему
"Нерешённые проблемы геометрии"
Во время Великой Отечественной войны в представлениях к полководческим
орденам писали: "Смело и решительно обходя очаги сопротивления,
не ввязываясь в затяжные бои, проник далеко вглубь обороны противника."
Так и математика ушла далеко вперёд: в некоторых областях, чтобы понять
условия задач, нужно учить лет десять специальный язык сложнее китайского.
Прорвавшаяся вперёд наука оставила очаги сопротивления даже в элементарной
геометрии: точки, прямые, окружности --- условия некоторых интересных понятны
даже школьнику, а решать их никто не умеет. Вот несколько таких неподдающихся
задач.
Каково минимальное число цветов, в которые можно так раскрасить плоскость,
чтобы концы любого отрезка длины 1 были покрашены в разные цвета?
Существует ли раскраска точек пространства в 14 цветов,
чтобы концы любого отрезка длины 1 были разного цвета?
Сколько точек общего положения должно быть отмечено на плоскости,
чтобы среди них непременно нашлись вершины выпуклого шестиугольника?
В любом ли многоугольнике с зеркальными изнутри сторонами
можно так разместить лампочку,
чтобы он был освещён весь?
Можно ли несколькими кругами, зеркальными снаружи, не пересекающими друг друга
и даже
не касающимися, загородить горящую лампочку?
В любом ли многоугольнике с зеркальными сторонами
существует хотя бы один замкнутый
путь светового луча?
Существует ли многоугольник, копиями которого плоскость можно покрыть,
но только непериодическим образом?
Может ли выпуклый многогранник, которым можно замостить
всё пространство,
иметь больше 38 граней?
Какова фигура минимальной площади,
которой можно покрыть любой многоугольник
диаметра 1?
Какова фигура минимальной площади,
которой можно покрыть любую
фигуру периметра 1?
Сколь велика может быть площадь
$n$-угольника диаметра 1 при
данном $n$?
У любого ли выпуклого многогранника
существует развёртка без самопересечений?
Рассмотрим $n$ точек, не лежащих на одной прямой.
Обязательно ли среди них
найдётся точка, через которую проходит не менее $n$/3 прямых, соединяющих
её с остальными $n$ точками?
Лекцию
23 октября 2004 года с 16.10 до 18.00
в аудитории 16-24
главного здания МГУ на Воробьёвых горах
прочитает ведущий научный
сотрудник Математического института РАН,
профессор Независомого
московского университета,
доктор физико-математических наук
Максим Эдуардович Казарян
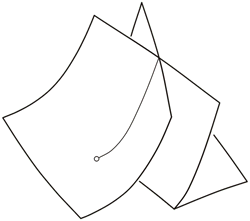
Тема лекции: ЛАСТОЧКИН ХВОСТ.
Это поверхность в пространстве многочленов вида
$x^4 + a x^2 + b x + c$, состоящая из троек $(a,b,c)$,
для которых многочлен имеет кратный корень. Эта поверхность
не является гладкой, и её особенности встречаются
во многих задачах дифференциальной геометрии и топологии.
Некоторые из них будут обсуждены на лекции.